I usually like Laetitia Vitaud’s writing on work, which combines a humane regard for people with a scepticism about large organisations and large tech. But there’s a line in her latest newsletter, which introduces a podcast with Azeem Azhar on his new book Exponential that jarred:

The gap between the way these services are delivered and the technologies we use on a daily basis is wider than it’s ever been. Though it’s likely to be worse in Germany than in many other places, there’s actually such a gap everywhere. Technologies continue to grow exponentially whereas our public services, traditional organisations, legal categories and social norms change much more slowly, in a linear fashion. (Her emphasis).

Obviously this is the thesis of the Azhar’s book, and in the newsletter we get the usual ‘exponential’ tropes: the ‘wheat and chessboard’ story, wheeled out to demonstrate that our brains aren’t equipped to think about exponential growth. (While checking this just now, I discovered that this story dates from 1256).

So maybe it’s worth interrogating the ‘exponential’ story and its limits. Here’s some quick notes.

First, this is a Silicon Valley story, driven by the fact that over quite a long period of time Moore’s ‘law’ anticipated that the number of transistors on a microchip doubled every year. And so it did—it was even baked into the industry roadmap. So people like the Singularity Hub imagined what would happen until At least, it did until it stopped doing it.

And for chips, there are some strong negative exponentials at work: for example, the cost of the fabrication plant for each new generation of chips doubles each time around—that gets pretty expensive pretty quickly.

Second, people imagine that—maybe because this is a ‘Silicon Valley is different’ story—that this exponential rule on technology improvement is specific to digital technologies. It’s not.

Research by the Santa Fe Institute found that Moore’s ‘Law’ was a version of ‘Wright’s Law’, developed in 1936 when microchips were the stuff of science fiction. The doubling effect is a function of economies of scale and scope (learning). There comes a point when you run out of scale.

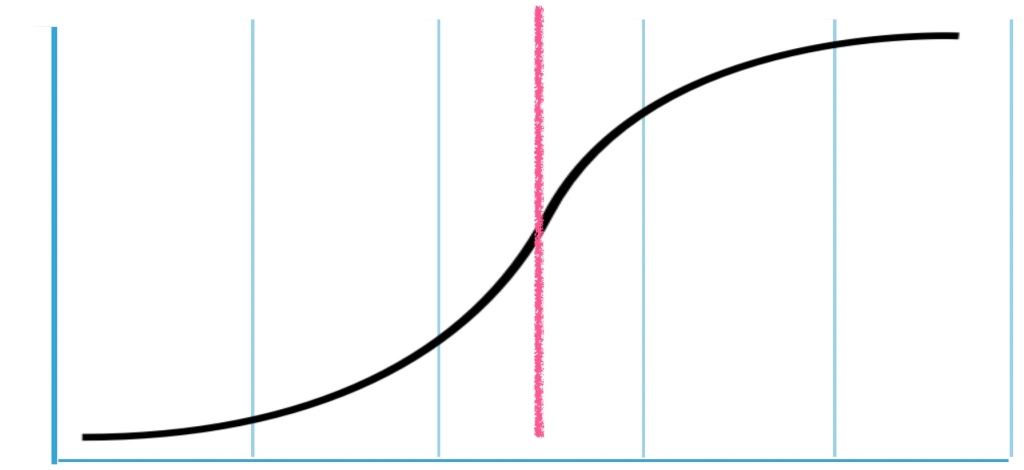
The mid-point is an inflection from acceleration to deceleration.

Third, and building on this, most technologies follow an S-curve pattern, accelerating towards a mid-point inflection and then slowing down. This is more obvious when you remember that an S-curve is the derivative of a diffusion curve; the mid point—at least when talking about markets—represents the point when half the available market has been reached.

But the reasons for that inflection point aren’t just to do with market capacity. The other thing that happens when technology applications accelerate rapidly is that they start to generate externalities, and these act as a brake on continuing accelerating growth. I wrote something about this in a piece reflecting on Alvin Toffler’s Future Shock, one of the 20th century ur-texts on the idea that change was going too fast for us to cope with:

S-curves or logistics curves, one of the basic building blocks of much futures thinking, show an acceleration in the first part of the S-curve, and then a deceleration in the second part. Much thinking that writes about exponential change, as Toffler does (in Future Shock) without using the word, imagines that the rapid acceleration seen in the second quartile of the S-curve, when growth is at its fastest, is a new normal, rather than a system that is about to start meeting its limits.

And if we look at the S-curve of technology and Vitaud’s ‘linear’ change in other social categories, we find that, in fact, regulation catches up. This is the reason why the question of how to manage our monopolistic tech giants is suddenly a live discussion.

The final note is a reflection on Stewart Brand’s ‘pace layers’ model, published in his book ‘The Clock of the Long Now’. The pace layers model looks like this:

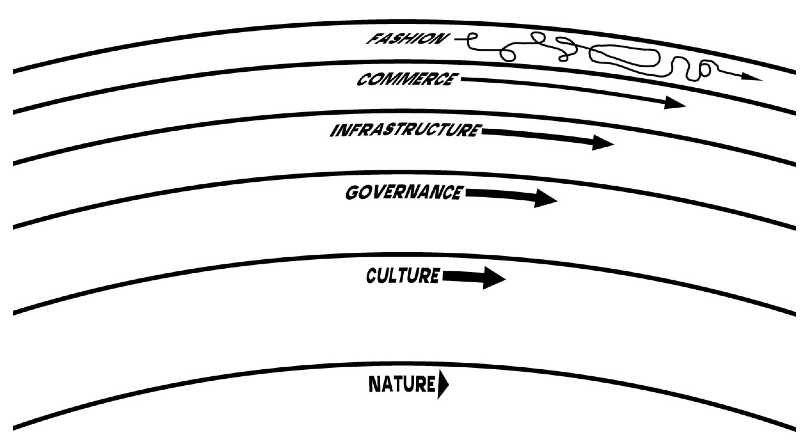
The pace layers. From Stewart Brand, The Clock of the Long Now.

Brand explains the difference between the top three layers (the fast layers, where tech also lives) and the bottom, ‘slow’, layers, like this:

Fast learns, slow remembers. Fast proposes, slow disposes. Fast is discontinuous, slow is continuous. Fast and small instructs slow and big by accrued innovation and by occasional revolution. Slow and big controls small and fast by constraint and constancy. Fast gets all our attention, slow has all the power. All durable dynamic systems have this sort of structure. It is what makes them adaptable and robust.

In an era of climate change, this is maybe a little more complex. Nature might be regulating the fast layers by being fast—even enforcing the occasional revolution. And indeed, Paul Saffo makes a similar point in a 2017 podcast conversation (57 minutes) with Stewart Brand about the pace layers, referencing the San Francisco earthquakes.

All the same, re-reading his article on this recently before I did some training, I was struck by a section in his final paragraph:

The division of powers among the layers of civilization lets us relax about a few of our worries.  We don’t have to deplore technology and business changing rapidly while government controls, cultural mores, and “wisdom” change slowly.  That’s their job.  Also, we don’t have to fear destabilizing positive-feedback loops (such as the Singularity) crashing the whole system.  Such disruption can usually be isolated and absorbed.  The total effect of the pace layers is that they provide a many-leveled corrective, stabilizing feedback throughout the system.

So why does the idea of ‘exponential’ continue to have such a hold? I have a benign version and a less benign version. The benign version is that humans are susceptible to the idea that ‘this time is different’. There’s a reason why ‘The Emperor’s New Clothes’ is such a compelling story. The less benign version: ‘exponential’ is an effective sales tool for consultants and technologists alike.

A shorter version of this article was also published on my Just Two Things Newsletter.